Mathematics Problems, Puzzles, and Challenges
All of the problems below are of my own devising. I've tried to include problems of varying levels of difficulty and from diverse areas within mathematics. Comments are welcome.
Solutions
Note: Whenever a problem calls for a numerical solution, try to give an exact answer (i.e., in terms of elementary functions, radicals, standard numerical constants, etc.), as opposed to a decimal approximation, if possible. Unless specified otherwise, assume all numbers are in base 10 and are written out in ordinary standard notation.
1. Evaluate the following expression:
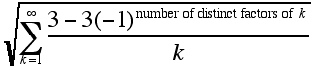
2. An "algebraic number" is defined as a number that is a zero of a polynomial function with integer coefficients. Thus the square root of 2 is algebraic, since f(x) = x2–2 evaluates to 0 if the square root of 2 is substituted for x. Similarly, the cube root of 2 is algebraic, since it is a zero of f(x) = x3–2. A theorem states that the sum of algebraic numbers must be an algebraic number. According to this theorem, 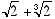 is algebraic. Find a polynomial function with integer coefficients that has
is algebraic. Find a polynomial function with integer coefficients that has 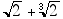 as a zero.
as a zero.
3. Let s be the sum of the units digits of the nth powers of 13 consecutive positive integers, the smallest of which is k. (n must also be a positive integer.) Find the minimum value for s; the minimum value for n that yields that value for s; and the minimum value for k that gives those values for s and n.
4. Evaluate the following expression:
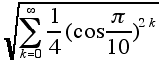
5. Evaluate the following expression:
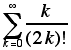
6. Evaluate the following expression:
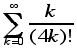
7. Skewes' Number, in its common form (using 10 as a base), equals 10101034.
How many distinct factors does the square root of Skewes' Number have?
8. How many distinct (i.e., mutually non-congruent) triangles are there such that, for each triangle, both of the following are true:
xxx• the side-lengths are integers in geometric progression
xxx• at least one side has length 100 ?
9. How many distinct (i.e., mutually non-congruent) triangles are there such that, for each triangle, both of the following are true:
xxx• the side-lengths are integers in arithmetic progression
xxx• at least one side has length 100 ?
The following two problems, and some subsequent ones, require the use of standard English words for the names of the counting numbers: "one," "two," "three," and so on. Please use the American system (e.g., 106 = one million, 109 = one billion, 1012 = one trillion), not the old British system. Example: 1,234,567,890,987,654,321 would be read as "one quintillion, two hundred thirty-four quadrillion, five hundred sixty-seven trillion, eight hundred ninety billion, nine hundred eighty-seven million, six hundred fifty-four thousand, three hundred twenty-one." For these problems, consider the names of only those positive integers that are between 1 and 1066–1, inclusive.
10. What number's name is first in alphabetical order among the perfect squares (in the specified set)?
11. What number's name is last in alphabetical order among the perfect squares (in the specified set)?
12. This one is basically a tedious exercise in silliness, but I'm including it anyway because it exhibits one of the most astonishing coincidences I've ever encountered. . . . .
Make a list of the names of the first 100 ordinal numbers. Your list should begin with "first," "second," "third," and end with "ninety-eighth," "ninety-ninth," "one hundredth."
Next, alphabetize this list. (I told you it was tedious!) Your new list should begin with "eighteenth," "eighth," "eightieth," and end with "twenty-seventh," "twenty-sixth," "twenty-third."
Now, down the left margin of a sheet of paper, write the 26 letters of the alphabet (in order), one per line.
Next to the letters, write the first 26 alphabetized number names in a column ("eighteenth" next to "A"; "eighth" next to "B"; and so on).
Then start a new column with the next 26 alphabetized number names ("fortieth" next to "A"; "forty-eighth" next to "B"; and so on).
Then start another new column with the next 26 alphabetized number names ("seventeenth" next to "A"; "seventh" next to "B"; and so on).
(There aren't enough number names remaining to make yet another complete column of 26, so don't bother.)
What number name concludes the first column?
What number name concludes the second column?
What number name concludes the third column?
13. Define n? for each positive integer n as follows:
xxxxxn? = 1+3+5+...+n, if n is odd;
xxxxxn? = 2+4+6+...+n, if n is even.
Evaluate
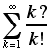 .
.
14. What are the coordinates of the incenter of a triangle whose vertices are at (3, 1), (5, 7), and (10, 3)? (Use ordinary rectangular coordinates.)
15. Solve each of the following equations for x (over the real numbers) so that the equation will be true for every integer n:
a)
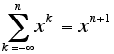
b)
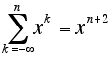
c)
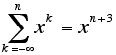
d)
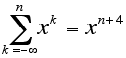
16. Begin a sequence (An) with a1 = 1; a2 = 1; a3 =1; then generate each subsequent term by taking the sum of the previous three terms (i.e., this is similar to the Fibonacci sequence except that three terms instead of two are added together). As the number of terms increases, the ratio between each term and its predecessor approaches a limit. Find this limit. I.e., find
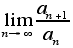
17. A type of challenge frequently seen in mathematical puzzle compendia requires the solver to construct expressions equal to various numbers, using a "tool kit" consisting of standard math symbols and some specified small number of repetitions of a particular digit. For example, I've seen (and tried my hand at) a challenge the object of which is to construct positive integers from four 4s and the symbols for addition, subtraction (unary "negative sign" OK), multiplication, division, factorial, and square root; as well as the decimal point and parentheses (for associative inclusion only [no combinatorics!]). Exponentiation and use of place value (base 10) are also allowed. Among those symbols and operations NOT allowed: combinations and permutations, subfactorial, greatest integer function, absolute value, bar or ellipsis for repeating decimal digits, radical symbol for roots other than square roots, conversion to non-decimal bases. Examples for the first few positive integers might be:
1 = (4/4)×(4/4)
2 = (4/4)+(4/4)
3 = (4+4+4)/4 , and so on.
a) Using only those symbols and operations specified above, and only TWO 4s, how many different integers between 0 and one googol, inclusive, can you construct? (I have found 62.)
b) Using those same symbols and operations, and still only TWO 4s, how many different non-integral rational numbers between .01 and 100 can you construct? (I have found 28.)
c) Using the same set of symbols and THREE 4s, find an expression that equals (the mathematical constant) pi.
d) Using the same set of symbols and FOUR 1s, find an expression that equals one quattuordecillion.
18. (Problem deleted)
19. What is the arithmetic mean of the set of all (nonzero) perfect squares less than or equal to one million? What is the median of this set?
20. (REVISED!) Suppose you perform an experiment as follows: roll an ordinary fair six-sided die and record the number k that comes up. Choose a random element x from the set whose members are all those numbers that are the product of k consecutive integers. What is the probability (over the entire experiment) that x is:
a) a positive number ending in 1? (i.e., the units digit is 1)
b) a negative number ending in 1?
c) a positive number ending in 2?
d) a negative number ending in 2?
e) a positive number ending in 3?
f) a negative number ending in 3?
g) a positive number ending in 4?
h) a negative number ending in 4?
i) a positive number ending in 5?
j) a negative number ending in 5?
k) a positive number ending in 6?
l) a negative number ending in 6?
m) a positive number ending in 7?
n) a negative number ending in 7?
o) a positive number ending in 8?
p) a negative number ending in 8?
q) a positive number ending in 9?
r) a negative number ending in 9?
s) a positive number ending in 0?
t) a negative number ending in 0?
u) equal to 0?
21. Let the "degrino" be a unit of angular measure that divides a circle into 20! (20 factorial) equal parts. For how many different values of n is the following statement true?
"The degrino measure of each interior angle of a regular n-gon is an integer."
22. Find the side-lengths of the triangle of minimum perimeter such that each side-length is a perfect square, and also the triangle is:
a) (no additional restrictions)
b) isosceles but not equilateral
c) scalene
d) right
e) acute
f) obtuse
g) obtuse and scalene
h) acute and scalene
23. How many cubic revo-Planck lengths are there in 1 cubic una-Hubble length?
24. In establishing the countability of the set of algebraic numbers (see #2 above), the mathematician Georg Cantor used a concept known as the "height" (sometimes called "weight") of a polynomial. Let us define the height of a polynomial with integer coefficients as follows:
"The height of a polynomial with integer coefficients is defined to be
the degree of the polynomial + the sum of the absolute values of the integer coefficients – 1 ."
Example: The height of x2–3x–1 would be 2+(1+3+1)–1, which equals 6 .
How many distinct polynomial expressions in x are there of height 10? (Rearrangement of terms does not count as distinct!)
25. A tire commercial claimed: "1 out of every 4 vehicles on the road has at least one underinflated tire." Suppose this is true. For this problem, assume each vehicle has exactly 4 tires. Assume also that underinflation is a random event whose probability is the same for all tires. What proportion of all tires (on vehicles on the road) is underinflated?
26. Suppose you are at P on the earth's surface, and your friend is at Q. Points P and Q are both in the Northern Hemisphere, and also both are in the Eastern Hemisphere. The east longitude of P is three times the north latitude of P. The north latitude of P is twice that of Q; the east longitude of Q is twice that of P. The geodesic (i.e., great-circle) distance between P and Q is 1500 miles. Assume the earth is a smooth sphere of radius 3963 miles. How would you and your friend exchange greetings in the native tongues of your respective localities?
27. How many distinct (i.e., mutually non-congruent) triangles are there such that, for each triangle, all of the following are true:
xxx• the degree measure of each angle is a perfect square
xxx• at least one side-length is a perfect square
xxx• the perimeter is less than 1000 ?
28. Find a polynomial function f such that the tangent lines to the graph of f at (1, f(1)), (2, f(2)), (3, f(3)), and (4, f(4)) enclose a square whose area is the arithmetic mean of f(1), f(2), f(3), and f(4).
29. I finished high school in 1974 and graduate school in 1979. In honor of these dates, find the distance between the parallel lines with equations
y = 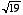 x +74
x +74
and
y = 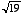 x +79 .
x +79 .
30. a) How many distinct (i.e., mutually non-congruent) triangles are there such that, for each triangle, all of the following are true:
xxx• the radian measures of at least two angles are integers
xxx• the perimeter is a perfect square
xxx• the perimeter is less than 1000 ?
......b) Of the set of triangles satisfying the conditions specified in part a), consider the one with maximum area. What is its perimeter? Its angle-measures? Its side-lengths? Its area?
31. In a right triangle of area 1, the hypotenuse is 1 unit longer than one of the legs. What is the perimeter of the triangle?
32. An equilateral triangle has area 1. A circle (in the same plane) whose center is coincident with the triangle's circumcenter intersects the triangle in such a way that all its arcs whose endpoints are consecutive points of intersection between the circle and triangle are congruent. It is neither the inscribed circle nor the circumscribed circle of the triangle. What is the radius of this circle?
33. A square has area 1. A circle (in the same plane) is concentric with the square and intersects it in such a way that all its arcs whose endpoints are consecutive points of intersection between the circle and square are congruent. It is neither the inscribed circle nor the circumscribed circle of the square. What is the radius of this circle?
34. (For this problem, "log" and "logarithm" refer to common [base-10] logarithms; "average" refers to arithmetic mean.)
I once ran a computer program to calculate the average logarithm of all 1-digit (positive) integers; of all 2-digit integers; and so forth. The calculations indicated an average log for 1-digit integers of approximately 0.61775; the average was 1.67122 for 2-digit integers, 2.67626 for 3-digit integers, and 3.67676 for 4-digit integers. I conjectured that the mantissas (the quantities after the decimal points) might be approaching a limit. Some subsequent analysis showed this to be true.
Let mn represent the average log of all n-digit integers (for positive integral n).
What is 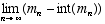 ?
?
35. Line L1 has the equation y = mx+1. Line L2 has the equation y = mx+2 (same m as for L1). m is a positive number such that the region within the second quadrant that is between L1 and L2 has area 1. What is the perimeter of this region?
36. Consider the function S that associates with each positive integer n the sequence containing the numbers of factors (divisors) of each of the positive integers between 1 and n, inclusive. For example, S(6) would be (1, 2, 2, 3, 2, 4). What is the smallest value of n for which S(n) has a single mode, and that mode is greater than 2?
37. a) What is the smallest positive integer that has exactly 100 distinct factors?
xxxb) What is the smallest positive integer that has more than 100 distinct factors?
38. A four-digit (base-10) integer is chosen at random. What is the probability there will be more 1s than 2s among its digits?
39. This question, like Problems 10, 11, and 12 above, involves the names in the American system for the positive integers less than 1066. (The principles of construction of these names can also be found in large dictionaries [e.g., Webster's Third New International Dictionary at the entry for "number"].) If the set of names of the first 1066–1 cardinal numbers (one, two, three, etc.) is alphabetized, the list will begin with "eight." But if the ordinal forms (first, second, third, etc.) are alphabetized, "eighth" will not be the first entry.
xxxa) In an alphabetical list of the names in the American system of the first 1066–1 ordinal integers, what name will be first?
xxxb) What position on such a list of alphabetized ordinals is occupied by "eighth"?
40. a) For how many integer values of n in the range 1 to 1000 (inclusive) is the following statement true?
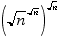 is an integer.
is an integer.
b) (NEW!) Among all the integer values for the expression shown in part a) (i.e., those that correspond to values of n that satisfy the conditions stated), which one has the most factors? How many?
41. What is the smallest positive integer that includes among its factors at least 10 perfect squares?
42. a) How many distinct (i.e., mutually non-congruent) triangles are there such that, for each triangle, both of the following are true:
xxx• at least two sides are congruent, and the length of each of the congruent sides is a 1-digit integer
xxx• the area is an integer ?
......b) Of the set of triangles satisfying the conditions specified in part a), consider the one(s) with maximum area. Give the perimeters of all such triangles.
43. What is the area (to the nearest square unit) of the violin on my home page? (It is bounded by x = –32 and x = 32.)
44. How many n-digit positive integers include exactly two 1s among their digits?
45. A real number x that is (strictly) between 0 and 10 is chosen at random. Let x' be the number that results when the integer part of x is multiplied by 10 but the fractional part remains the same. (Example: If x is 3.462, then x' would be 30.462.) What is the expected value of x'/x?
46. Consider the set of all quantities p/q such that p and q are integers, 0 < p < q < 1,000,000, and the decimal representation of p/q terminates. What is the maximum of this set?
47. The degree measures of the angles of an acute triangle are all prime numbers. One side—not the shortest—has length 1. What is the area of the triangle?
48. a) How many different combinations of three integers could represent the degree measures of the angles of a triangle?
b) In how many of these combinations are all three integers prime?
49. The maximum possible number of angles of a scalene triangle have degree measures that are perfect numbers. What is the minimum possible area of the triangle if the perimeter is also a perfect number?
50. Mathematician A says, "I'm thinking of an integer k. I'll show you only the units digit of the product of k × (k+6), and you should be able to tell me what k is." Mathematician B responds, "You don't need to show me anything—I already know." What is k?
51. (REVISED!)
a) All the edges of a regular pentagonal pyramid have length 1. What is the volume of the pyramid?
b) All the edges of a regular pentagonal pyramid are congruent. The volume of the pyramid is 1. What is the length of each edge?
52. Give all values of n for which the following statement could be true:
The degree measures of the angles of an n-gon are consecutive integers.
53. Consider the names of the integers between 1 and 1,000,000, inclusive. Of these:
a) how many are spelled with more consonants than vowels?
b) how many are spelled with an equal number of consonants and vowels?
c) how many are spelled with more vowels than consonants?
54. Consider the set of names of the integers between 1 and 1066–1, inclusive. For each member of the set, let C = the number of consonants and V = the number of vowels.
a) What is the minimum value of C–V?
b) How many members of the set have this value?
55. x, y, and z are positive real numbers. x < y < z, and x+y+z = 10.
a) Give the ranges of possible values for x, for y, and for z.
b) Same as a), but with the added condition that at least one of x, y, or z must be an integer.
c) Same as a), but with the added condition that at least two of x, y, and z must be integers.
d) Same as a), but with the added condition that x, y, and z must be integers.
56. Find 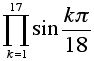 .
.
57. k distinct positive numbers, of which exactly j are integers, sum to 10. Describe the set of all possible ordered pairs (j, k).
58. Five integers are chosen at random. What is the probability that at least one of the following is true?
1) One or more of the integers is a multiple of 10.
2) The members of at least one pair of those integers differ by a multiple of 10.
59. Define round(x) as the closest integer to x.* Find the total length of all intervals of x values in which round(x2) and round(x) are both positive numbers that have the same number of digits.
*Solving this problem doesn't require specifying whether half-integers are rounded up or down, but if you wish to make the definition unambiguous you are welcome to choose one or the other!
60. Consider the standard names (in American English) of the positive integers that are between 1 and 1066–1.
a) What number's name is first in alphabetical order among the factorials (in the specified set)?
b) What number's name is last in alphabetical order among the factorials (in the specified set)?
61. Consider the standard names (in American English) of the positive integers that are between 1 and 1066–1, . . . spelled backwards.
a) What number's name is first in alphabetical order (in the specified set)?
b) What number's name is last in alphabetical order (in the specified set)?
62. How many distinct (i.e., mutually non-congruent) triangles are there such that, for each triangle, all of the following are true:
• the radian measures of at least two angles are integers
• the length of at least one side is an integer
• the perimeter is less than 100 ?
63. How many five-digit integers (in base 10) are powers of smaller integers?
64. On an ordinary set of x–y coordinate axes, place a unit circle with its center at the origin. Find the coordinates of a point (p, q) on the circle such that the tangent to the circle at (p, q) contains a segment of length 5 that lies in the first quadrant and whose endpoints are on the axes.
65. Let S be the sum of the degree measures of all the interior angles of an n-sided polygon.
a) What is the minimum possible value of n for which the sum of the digits of S is at least 100?
b) What is the maximum possible value of n for which the sum of the digits of S is less than 10, and no digit of S other than the units digit is 0?
c) What is the maximum possible value of n for which the digits of S are all distinct?
d) For what value of n would the name of S be the first in alphabetical order among all possible values of S when spelled out in English?
e) For what value of n would the name of S be the last in alphabetical order among all possible values of S when spelled out in English?
f) What is the minimum possible value of n for which the name of S, when spelled out in English, contains the letter "L"?
g) Give a formula for n in terms of k such that the corresponding value of S will be the kth smallest perfect square among all possible values of S.
h) What is the maximum possible value of n for which the digits of S, read left to right, are strictly decreasing?
66. Consider the set of all quantities p/q such that p and q are integers, and 0 < p < q < 1,000,000. If the maximum of this set is represented in decimal form, how many factors does the product of the first 100 digits after the decimal point have?
67. a) In the decimal expansion of π, how many factors does the product of the first 10 digits after the decimal point have?
b) How many factors does the product of the first 100 digits after the decimal point have?
68. Consider the (infinitely) repeating decimal 0.123456789 123456789 123456789 ... .
a) How many factors does the product of the first 1000 digits after the decimal point have?
b) How many factors does the sum of the first 1000 digits after the decimal point have?
69. Four integers are chosen at random. What is the probability their product will end in 0?
70. Let A be the sequence whose nth element is the smallest n-digit positive integer the product of whose digits is an n-digit integer. List the entire sequence A.
71. Let f be the function on nonnegative integers such that f(n) is the base-10 number that results when each digit of n is replaced by its equivalent in binary. (Example: f(27) = 10,111.)
a) What is the smallest n for which f(n) exceeds a googol?
b) For how many different values of n does f(n) = 11,111? What is the smallest such n?
72. Suppose you have an ordinary old-fashioned nondigital clock (with the numbers 1 through 12 spaced evenly around the circumference of a circular face [12 at the top, if you like], and an hour hand and a minute hand that rotate continuously at a constant rate). For this problem, let the time always be expressed as a whole number of hours and a precise number of minutes. (Example: At 2:05 and 15 seconds, the time would be given as 2 hours, 5.25 minutes.)
a) When would be the first time after 12:00 that the measure, in degrees, of the smaller angle between the hour hand and the minute hand would equal the sum of the hour and the minutes past the hour? When would be the second time? The third?
b) When would be the first time after 12:00 that the measure, in degrees, of the smaller angle between the hour hand and the minute hand would equal the product of the hour and the minutes past the hour? When would be the last time before 12:00 that the measure, in degrees, of the smaller angle between the hour hand and the minute hand would equal the product of the hour and the minutes past the hour?
73. How many different multisets of positive integers can be constructed each having the property that 36 is both the sum and the product of all its elements? (A multiset is just a set where repeated elements are allowed.) List them.
74. Each of a and b is a randomly selected positive integer. What is the probability that the units digit of ab is:
a) 1?
b) 2?
c) 3?
d) 4?
e) 5?
f) 6?
g) 7?
h) 8?
i) 9?
j) 0?
75. For how many positive integers less than or equal to 1,000,000 is the product of the digits a power of 8? (Note: 80 and 81 count as powers.)
76. a) What is the smallest positive integer the product of whose digits is (exactly) a googol?
b) What is the smallest positive integer the product of whose digits is greater than a googol?
77. a) What is the smallest positive integer such that the product of its digits equals 1,000,000, and no digit appears twice in a row?
b) The largest?
78. What is the smallest positive integer such that the sum of its digits equals 100, and no digit appears twice in a row?
79. How many elements are in the set that consists of every distinct quantity that is the average (arithmetic mean) of the digits of an integer between 1 and 1,000,000, inclusive?
80. a) For how many integers between 1 and a googol (inclusive) is the product of the digits a prime number?
b) For how many integers between 1 and a googol (inclusive) is the product of the digits a one-digit positive number?
81. a) What is the smallest positive integer for which the product of its digits is exactly 100 times the sum of its digits?
b) What is the smallest positive integer for which the product of its digits is more than 100 times the sum of its digits?
82. How many positive integers have 100 as both the sum and the product of their digits?
83. Find the smallest positive integer N such that if a positive integer k that is less than or equal to N is selected at random, the probability is greater than not that the digits of k will include:
a) at least one 0.
b) at least one 1.
84. Find the smallest positive integer N such that if a positive integer k that is less than or equal to N is selected at random, the probability that all the digits of k will be the same is greater than the probability they will all be different.
85. Consider the set of positive integers for which there are, among the digits of each:
• more 0s than 1s;
• more 1s than 2s;
• more 2s than 3s;
• more 3s than 4s;
• more 4s than 5s;
• more 5s than 6s;
• more 6s than 7s;
• more 7s than 8s; and
• more 8s than 9s.
a) What is the smallest such integer?
b) What is the largest such integer that is less than a googol?
86. Let P be the product of all the distinct factors of 100! (100 factorial). P has d digits, the last k of which are 0s. What is d, and what is the maximum value of k?
87. Find the longest sequence of consecutive integers such that the product of their factorials is a factor of 100!.
88. In the decimal expansion of π, what is the sum of the first 500,000 digits after the decimal point? Express your answer in scientific notation, accurate to three significant digits.
89. What is the sum of the digits of the number that is equal to 10100–1099–1098
– . . . –101–100 ?
90. Find the smallest integer x for which each statement is true, with x, a, b, c, and d all distinct:
a) x has a (distinct) factors. a has b factors. b has c factors. c has d factors.
b) x has a digits. a has b digits. b has c digits. c has d digits.
91. Find the smallest integer that is divisible by:
a) every positive even integer less than 100.
b) every positive odd integer less than 100.
92. What is the smallest four-digit prime number whose digits alternate in parity (i.e., being even or odd)?
93. a) How many six-digit positive integers have the property that the sum of their digits is greater than the product of their digits?
b) Among those, how many do not contain the digit "0"?
94. Consider those prime numbers that have more even digits than odd digits.
a) What is the smallest?
b) The second smallest?
c) The largest that is less than 1,000,000?
95. a) What is the largest integer not containing the digit "1" for which the product of its digits equals the factorial of any integer?
b) Let k be the integer whose factorial is the product of the digits of the answer to part a). What is the smallest integer the product of whose digits equals k! ?
96. a) Let P(k) denote the product of the digits of k, where k is any positive integer. How many different values of P(k) less than or equal to 1,000,000 can be generated from only those values of k that have all even digits?
b) Let S be the set of all values of P(k) that satisfy the conditions stated in part a). Let M be the maximum element of S. What is M?
c) For how many different values of k with all even digits does P(k) equal M? What is the smallest such k? The largest?
97. An integer between 1 and 1,000,000 (inclusive) is chosen at random, and its digits are multiplied together. Give, as an exact percentage, the probability that the product will be:
a) an odd positive number;
b) an even positive number;
c) neither.
98. Define a sequence A as follows:
A(1) = 1 ;
A(n+1) = A(n) + the least integer greater than A(n) that has no digits in common with it.
a) What is A(100) ?
b) Find a closed-form formula for A(n) (i.e., using only standard mathematical functions and symbols).
99. Begin with any integer n > 1. Take the integer part of its square root. Repeat the operation with the new result. Continue this process until you reach 1.
a) How many steps will it take to reach 1, as a function of n? (Do not count the starting number as a step.)
b) How many digits are in the smallest n that requires 10 steps to reach 1? What is the last digit of n?
100. An integer between 1 and 1,000,000 (inclusive) is chosen at random. Give, as an exact percentage, the probability that it will have:
a) more even digits than odd digits;
b) more odd digits than even digits;
c) an equal number of even and odd digits.
101. An integer between 1 and 1,000,000 (inclusive) is chosen at random. Give, as an exact percentage, the probability that the product of its digits will be:
a) a multiple of 6, if 0 counts as a multiple;
b) a positive multiple of 6;
c) not a multiple of 6.
102. For how many integers between 1 and 1,000,000 is the sum of their digits at least 50?
103. How many integers between 1 and 1,000,000 have the property that both the sum and product of their digits are prime numbers? List them.
104. What is the sum of the last 25 digits of the 158-digit number that equals 100! ?
(Obviously, one can "solve" this by just looking up the value of 100! online. But is there a relatively quick way to solve it using mathematical properties, that could be done with pencil and paper? [Hint: Yes.])
105. Construct the set whose elements are those integers between 1 and 1,000,000 for which the product of their digits equals 1,000.
a) How many elements are in the set?
b) What is the median of the set?
c) What is the expected sum of the digits of a randomly chosen element of the set?
d) If a single digit from one of the elements of the set is chosen at random, what is its expected value?
106. The circumference of a unit circle is 2π, or approximately 6.2831853072. The perimeter of a convex polygon inscribed in a unit circle will be less than 2π, but as the number of sides increases the perimeter will approach that value. What is the minimum n such that the perimeter of a regular n-gon inscribed in a unit circle will be greater than or equal to:
a) 6?
b) 6.2?
c) 6.28?
d) 6.283?
e) 6.2831?
f) 6.28318?
107. a) Suppose a person decided to write out every integer from 1 to 1,000,000 (without commas), and they could write at an effective rate of two digits per second (i.e., taking into account all extraneous factors). If they were able to devote two hours a day to this effort, how long would it take from start to finish?
b) Suppose they wanted to write out the first million numbers, but in binary instead of decimal. (Here, "million" still means the same as it did in part a): the decimal number 1,000,000.) At the same rate — two (binary) digits per second, two hours a day — how long would that take?
c) Suppose they just wanted to write all the integers in binary up to 10000002. Writing at the same rate as before, how long would that take?
108. a) What is the 1,000,000th smallest positive integer among those whose 1,000,000th powers have "1" as their units digit?
b) Let N be the answer to part a). How many digits does N1,000,000 have?
109. What is the largest integer less than or equal to a googol in which each of the digits 0 through 9 appears at least once, with each prime digit occurring a composite number of times and each composite digit occurring a prime number of times?
110. What is the maximum sum of the digits among the members of the set of n-digit integers with all digits distinct? Express your answer as a polynomial in n.
111. What is the smallest integer the sum of whose digits is a pandigital number (i.e., the sum contains each of the digits 0 through 9 at least once)?
112. What is the smallest pandigital integer the sum of whose digits is pandigital?
113. Consider those ordered pairs of positive integers (x,y) that satisfy all the following conditions:
• x/y = a 1-digit integer;
• x–y = a 2-digit integer;
• x+y = a 3-digit integer;
• xy = a 4-digit integer.
a) What pair includes the smallest possible x?
b) What pair includes the largest possible x?
c) What pair includes the smallest possible y?
d) What pair includes the largest possible y?
114. What is the limit, as n increases without bound, of the product of all the odd digits among the first n digits after the decimal point in the decimal expansion of π?
115. From the set of prime numbers less than 1,000, two primes are chosen at random. Give the probability in terms of "1 in n," where n is the nearest integer, that the units digit of the product of the chosen primes is:
a) 0
b) 1
c) 2
d) 3
e) 4
f) 5
g) 6
h) 7
i) 8
j) 9
116. Find the minimum positive integer k that makes the following statement true:
The probability that a randomly-selected positive integer will be divisible by each positive integer less than or equal to k is less than 1 in 1,000,000.
117. Let Sn,L be the sum of the first L digits following the decimal point in the decimal expansion of 1/n (* see note below). For what value of n (among all positive integer values) is Sn,L maximized for all sufficiently large L?
Note: For this problem, any value that can be expressed as a terminating decimal must be so expressed (with 0s for all trailing digits). For example, while it is true that 1/2 = 0.4999..., for this problem 0.5000... should be used.
118. Define a proper fraction as a ratio p/q, where p and q are positive integers, and p < q. Such fractions are named in English according to the following conventions:
• first, the numerator is spelled out;
• then, the denominator is spelled out in its ordinal form;
• if the numerator is greater than 1, an s is added to the end of the ordinal form of the denominator (to make it plural).
• Exception: 1/2 is written as one half (not "one second").
Using the above conventions, find:
a) the smallest proper fraction in lowest terms whose spelling does not include the letter n;
b) the largest.
119. How many different ordered triples (a,b,c) are there such that a, b, and c are integers, and abc = 24?
120. What is the smallest integer n for which at least half of the factors of n! are multiples of 100?
121. What is the smallest integer n for which at least 90% of the factors of 10n are multiples of 100?
122. How many distinct factors does googol – (0.1 × googol) have?
123. a) How many positive integers less than or equal to 1,000,000 have the property that each of its digits appears a number of times equal to itself? (For example, if any of its digits are 2s, it must have exactly 2 of them.)
b) (NEW!) How many positive integers less than or equal to 1,000,000 have the property that any digit d that appears within it occurs dk times, where k can be any integer? (Note: For this problem, consider 00 to be undefined.)
124. a) Consider those positive integers with all even digits. For how many of these is the product of the digits a number with exactly 10 distinct factors?
b) How many of those (that satisfy the conditions in part a)) have all distinct digits? List them.
c) How many of them (those that satisfy the conditions in part a)) have all their digits the same? List them.
125. For how many positive integers less than or equal to 1,000 does the product of the digits have an odd number of factors?
126. Consider the set of those positive integers with all distinct digits (i.e., no digit occurring more than once).
a) What is the maximum possible number of factors of the sum of the digits of any member of this set?
b) How many elements of this set have that number of factors for the sum of their digits? What is the smallest such element? The largest?
127. For this problem, consider a standard notation that is used in the U.S. to show calendar dates: mm/dd/yyyy. Example: As I am typing this, the date is January 10, 2024, which would be shown as 01/10/2024. Note that leading 0s are used to "fill out" single-digit months or days to two digits.
a) If all the digits of today's date (ignoring the forward slashes) are multiplied together, the product will be 0. In fact, this will continue to be the case for quite some time. When will be the next time the product of the digits of the date in mm/dd/yyyy format will be nonzero?
b) When will the product next be a 2-digit number?
c) A 3-digit number?
d) A 4-digit number?
e) A 5-digit number?
f) A 6-digit number?
128. Define the 20th century as the span of 100 calendar years that began on January 1, 1901.
a) What was the earliest date in the 20th century when all the digits in mm/dd/yyyy format were different?
b) If a date from the 20th century is chosen at random, what is the probability that the product of the digits (in mm/dd/yyyy format) will be nonzero?
c) What is the probability the product will be a one-digit positive number?
d) What is the probability the sum of the digits will be a one-digit positive number?
129. When was the first time within the lifetime of anyone who could possibly be reading this problem that the sum of the digits of the date in mm/dd/yyyy format was a one-digit number? When was the last time before that?
130. When was the last time that all eight digits of the date in mm/dd/yyyy format were different? When will be the next time?
131. a) For a given positive integer n, construct the set of circles with one each of radius 1 inch, 2 inches, 3 inches, ..., up to n inches. What is the minimum value of n so that the total of the circumferences of all the circles is greater than 1 mile?
b) What is the minimum value of n so that the total of the areas of all the circles is greater than 1 square mile?
132. a) What is the greatest positive integer less than a googol for which the sum of the digits and the product of the digits are both powers of 3?
b) For which both the sum and product of the digits are the same power of 3?
133. What is the minimum n such that a regular n-gon with each side measuring 1 inch will have an area that exceeds 1 square mile?
134. For how many positive integers less than or equal to a googol is the product of the digits a power of 2? (Note: 20 and 21 count as powers of 2.)
135. How many positive integers in the range 10 to 1,000,000 (inclusive) have the property that the sum of each pair of digits, whether adjacent or not, is prime? List them.
136. a) What is the smallest positive integer whose name, when spelled out in English, shares at least one letter with the name of every other number?
b) What is the largest integer whose name does not share at least one letter with every other number name?
(See the text preceding Problem 10 on this page for details regarding number names.)
137. Give all values of n for which the following statement is valid:
If an element is selected at random from the set of all n-digit positive integers, the probability that both the sum of its digits and the product of its digits will be odd numbers is greater than 1%.
138. Consider the set of all numbers that are the products of the digits of positive integers less than or equal to a googol. How many (distinct) members of this set are powers of primes? (Note: 0th and 1st powers count.)
139. Consider the set of all numbers that are the sums of the digits of positive integers less than or equal to a googol. How many (distinct) members of this set are powers of primes? (Note: 0th and 1st powers count.)
140. Find the smallest positive integer for which both the sum of its digits and the product of its digits are:
a) 1-digit integers.
b) 2-digit integers.
c) 3-digit integers.
141. Find the largest positive integer for which both the sum of its digits and the product of its digits are:
a) 1-digit positive integers.
b) 2-digit integers.
c) 3-digit integers.
142. For a and b positive integers, how many expressions of the form ab are equal to b-digit integers?
143. For how many positive integers less than or equal to 1,000,000 is the product of the digits a power of 6? (Note: 0th and 1st powers count.)
144. Consider the 1,000 functions of the form f(x) = ax2+bx+c, where each of a, b, and c is a positive integer less than or equal to 10. Which of these functions has the greatest real zero, and what is its value?
145. Let m and n be positive integers, m < n, such that their product, mn, is a 10-digit number.
a) What is the minimum value of m+n?
b) How many distinct pairs {m, n} give that minimum value for m+n?
c) Among those pairs, what is the minimum value of m?
146. Find positive integers a, b, c, d such that all of the following conditions hold:
• a < b < c < d ;
• (1/a)+(1/b)+(1/c)+(1/d) < 1 ; and
• a+b+c+d is the minimum possible.
147. Consider those positive integers that have an equal number of even digits (none of which may be 0) and odd digits, such that the sum of their digits is a three-digit number.
a) What is the smallest?
b) The largest?
c) How many such integers have the same number of digits as the answer to part a)? (Include the answer to part a) in your count.)
148. Consider those positive integers that have (exactly) twice as many odd digits as even digits. For how many of these is the sum of their digits a three-digit prime number?
149. Consider those positive integers that have an equal number of even digits and odd digits, such that the product of their digits is a three-digit number.
a) What is the smallest?
b) The largest?
150. How many 100-digit positive integers have cube roots that have an odd number of factors?
151. If the calendar months are numbered in the customary way (January = 1, February = 2, and so forth):
a) When was the last time it was the case that monthday = year?
b) When will be the next time?
152. In a right triangle, the angle measures are in geometric progression. What are the degree measures of the acute angles?
153. For every positive integer n, define f(n) as follows:
If n is a one-digit number, f(n) = n. If n has more than one digit, raise the first (leftmost) digit of n to the power of the second digit. If there are subsequent digits, raise that result to the power of the third digit, and so on until all digits are used. The final result is f(n).
Example: f(3472) = ((34)7)2. (That is, 523,347,633,027,360,537,213,511,521.)
a) What is the smallest n for which f(n) exceeds 10?
b) What is the smallest n for which f(n) exceeds 100?
c) 1000?
d) 1,000,000?
e) googol?
f) List every two-digit integer that is equal to f(n) for some positive integer n.
g) For how many different values of n among the first 1000 positive integers (i.e., 1 < n < 1000) does f(n) equal 1?
h) For how many different values of n among the first googol positive integers does f(n) equal 1?
i) How many distinct factors does f(23456789) have?
154. What is the smallest pandigital palindromic prime number? (For this problem, "pandigital" means the number must contain each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 at least once.)
155. What is the smallest possible area of a right triangle in which the product of the degree measures of the acute angles, and also the length of at least one side, are integers?
156. Find the largest integer such that each pair of adjacent digits, if read as a two-digit number, is prime, and no such pair appears more than once.
(Examples: 123 would fail because 12 is not prime. 113 works, because both 11 and 13 are prime [but 113 is obviously not the largest solution!]. 1,113 would fail because "11" appears more than once.)
157. Find the smallest positive integer that has more odd digits than even digits, such that the sum of its digits is:
a) prime.
b) a 2-digit prime.
c) a 3-digit prime.
Solutions
Back to my home page.
Back to my main links page.
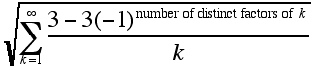
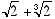 is algebraic. Find a polynomial function with integer coefficients that has
is algebraic. Find a polynomial function with integer coefficients that has 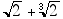 as a zero.
as a zero.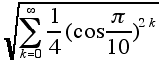
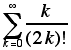
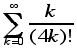
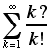 .
.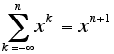
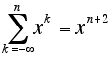
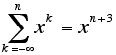
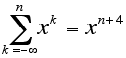
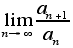
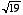 x +74
x +74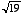 x +79 .
x +79 .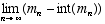 ?
?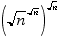 is an integer.
is an integer.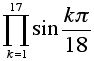 .
.