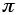
2. f(x) = x18–12x15+36x12–2560x9–13104x6–17472x3–64 is one such function.
.......Update: Acknowledgements to correspondent Jeremy Weissmann, who found the following polynomial of degree 6:
.......f(x) = x6–6x4–4x3+12x2–24x–4 .
3. s = 35 ; n = 4 ; k = 9
4.
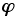, or phi, also known as the golden ratio or golden section. It is equal to 
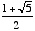.5. (sinh 1)/2
6. (sinh 1–sin 1)/8
7.
8. 11
9. 182
10. 8,018,844,304 (eight billion, eighteen million, eight hundred forty-four thousand, three hundred four), which is the square of 89,548.
11. 2,000,000,000,000,000,000,000,000,002,202,211,698,297,079,027,232,663,249,060,167,009 (two vigintillion, two undecillion, two hundred two decillion, two hundred eleven nonillion, six hundred ninety-eight octillion, two hundred ninety-seven septillion, seventy-nine sextillion, twenty-seven quintillion, two hundred thirty-two quadrillion, six hundred sixty-three trillion, two hundred forty-nine billion, sixty million, one hundred sixty-seven thousand, nine), which is the square of 44,721,359,549,995,793,928,183,473,399,247.
12. "first";"second";"third"
13. e + (sinh 1)/4
14. I found a formula on an internet site,
http://mathforum.org/dr.math/faq/formulas/faq.analygeom_2.html#twotriangles ,
which aided me in determining the correct solution:
(
, 
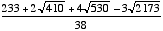).Before finding the above formula I had gotten the solution simplified only to the point shown below after many attempts over many years:
Incenter is at (x0, y0), where
x0 =
3 +
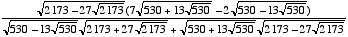,and y0 =
.15. a) 2
b)
(see #4 above)c)
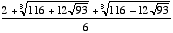
d)
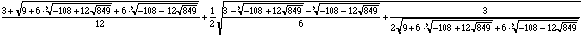
16.
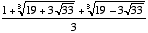
17. a) I found expressions for 0, 1, 2, 4, 5, 6, 8, 10, 12, 16, 20, 22, 24, 26, 28, 44, 48, 60, 64, 96, 120, 256, 576, 720, 4096, 13824, 40320, 331776, 3628800, 16777216, 191102976, 479001600, 20922789888000, 281474976710656, 36520347436056576, 2432902008176640000, 1124000727777607680000, 25852016738884976640000, 155112100433309859840000, 248179360693295775744000, 310224200866619719680000, 620448401733239439359976, 620448401733239439359996, 620448401733239439359998, 620448401733239439360000, 620448401733239439360002, 620448401733239439360004, 620448401733239439360024, 1240896803466478878720000, 1551121004333098598400000, 2481793606932957757440000, 14890761641597746544640000, 403291461126605635584000000, 304888344611713860501504000000, 1333735776850284124449081472843776, 384956219213331276939737002152967117209600000000, 2658271574788448768043625811014615890319638528000000000, 12413915592536072670862289047373375038521486354677760000000000, 238845470948181951014676282087587661242764623832882511609856000000000000, 8320987112741390144276341183223364380754172606361245952449277696409600000000000000, 126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000, and 148191290711022364575836328127140926575194970820976779184863158185815504490332160000000000000000.
Click here to view.
b) I found expressions for 1/64, 1/60, 16/625, 1/24, 1/16, 8/125, 1/12, 1/10, 1/8, 4/25, 1/6, 1/5, 1/4, 2/5, 11/25, 1/2, 4/5, 8/5, 12/5, 5/2, 18/5, 22/5, 25/4, 48/5, 125/8, 118/5, 122/5, and 625/16.
Click here to view.
c)
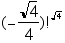would work.d)
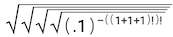
18. (Problem deleted)
19. The mean is 333833.5 ; the median is 250500.5 .
20. a) 1/120 b) 1/120 c) 3/40 d) 1/120 e) 1/120 f) 1/120 g) 7/120 h) 1/40 i) 1/120 j) 1/120 k) 7/120 l) 1/40 m) 1/120 n) 1/120 o) 1/120 p) 1/120 q) 1/120 r) 1/120 s) 61/120 t) 17/120 u) infinitesimal
21. 41,038
22. a) 1, 1, 1
xxxb) 1, 4, 4
xxxc) 16, 25, 36
xxxd) no solution (this is easily proven using the Pythagorean Theorem and Fermat's Last Theorem!)
xxxe) 1, 1, 1
xxxf) 9, 9, 16
xxxg) 16, 25, 36
xxxh) 64, 81, 100
23. Since the Hubble length is not defined with great precision, an exact answer is not possible. However, the answer would be roughly on the order of 10385.
24. I counted 11,148.
25.
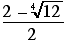
26. You could say either "Bonjour!" (in French, the official language) or "Bara ala!" (in Sango, the national language) from your position at about 7.2ºN, 21.5ºE in Central African Republic. Your friend would likely reply "Asalaamu Aleikum" (in Arabic), or perhaps "Nabad" (in Somali), from his or her position at approximately 3.6ºN, 43.0ºE in Somalia.
27. 52
28. One such function would be:
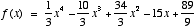,which includes the points (1,
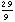), (2, 
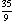), (3, 
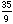), and (4, 
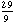); the tangents at these points enclose the square with vertices (
, 
), (
, 
), (
, 
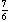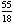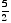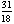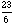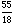), and (
, 
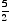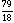), which has area 
.29.
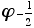(see #4 above)30. a) 62
......b) Perimeter = 961; Angle measures (in radians): 1, 1, and
; Sides: two each measuring 961/(2 + 2 cos 1), and one measuring (961 cos 1)/(1 + cos 1); Area: (923521 sin 2)/(12 + 16 cos 1 + 4 cos 2)
31.
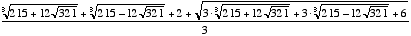
32.
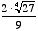
33.
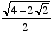
34.
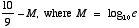
35.
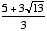
36. 35
37. a) 45,360
b) 50,400 (which has 108 factors)
38.
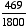(2345 out of 9000)39. a) eight billion, eighteen million, eighteenth
b) "Eighth" is the 1,001,001,001,001,001,001,001,002,001,002,001,001,001,001,001,001,001,002,001,001,002nd entry on the list.
40. a) 516
b)
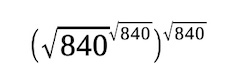, which has 94,093,879,321 factors
41. 2304
42. a) 276
b) Each of two distinct triangles has the maximum area: one with perimeter
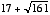and one with perimeter 
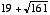.43. 688
44. 9n–3(4n2–3n–1)
45. 1 — 0.9 ln 9! + 8.1 ln 10
46. 819199/819200 (which equals exactly 0.999998779296875)
47. (sin 2°)/2
48. a) 2700
b) 7
49.
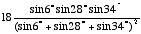
50. –3
51. a)
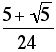, which can also be expressed as 
, 
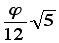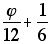, or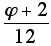 
b)
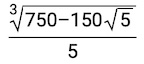
52. 3, 5, 9, 15, 16. A very liberal interpretation of the conditions might also allow polygons of 48, 80, 144, and 240 sides. I choose not to consider these, since each would require a 180° angle to be regarded as an interior angle of a polygon. . . . One might also argue that one 180° angle could be counted, but since the "sides" meeting at its vertex would be collinear, they could be combined to make one side, resulting in polygons of 47, 79, 143, and 239 sides possibly satisfying the conditions. (I would still be inclined to reject such an argument.)
53. a) 999,968
b) 29
c) 3
54. a) –2
b) 37,748,736
55. a) 0 < x < 10/3; 0 < y < 5; 10/3 < z < 10
b) 0 < x < 3; 1/2 < y < 5; 7/2 < z < 9
c) x = 1, 2, or 3; y = 1, 2, 3, or 4; z = 4, 5, 6, 7, or 8
d) x = 1, 2, or 3; y = 1, 2, 3, or 4; z = 4, 5, 6, 7, or 8
56. 9/65536
57. Either:
j = k = 1, 2, 3, or 4;
or:
j = 0, 1, 2, or 3; and k is any integer that exceeds j by at least 2.
58. 1061/1250, or .8488
59.
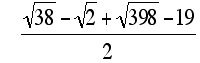
60. a) 8,222,838,654,177,922,817,725,562,880,000,000 (eight decillion, two hundred twenty-two nonillion, eight hundred thirty-eight octillion, six hundred fifty-four septillion, one hundred seventy-seven sextillion, nine hundred twenty-two quintillion, eight hundred seventeen quadrillion, seven hundred twenty-five trillion, five hundred sixty-two billion, eight hundred eighty million), which is 31!.
b) 2,658,271,574,788,448,768,043,625,811,014,615,890,319,638,528,000,000,000 (two septendecillion, six hundred fifty-eight sexdecillion, two hundred seventy-one quindecillion, five hundred seventy-four quattuordecillion, seven hundred eighty-eight tredecillion, four hundred forty-eight duodecillion, seven hundred sixty-eight undecillion, forty-three decillion, six hundred twenty-five nonillion, eight hundred eleven octillion, fourteen septillion, six hundred fifteen sextillion, eight hundred ninety quintillion, three hundred nineteen quadrillion, six hundred thirty-eight trillion, five hundred twenty-eight billion), which is 44!.
61. a) 300 (three hundred, which spelled backwards is derdnuh eerht).
b) 660,000,000,000,000,000,000,000,000,000,000,000,000,060,060,000,000,000,000,000,000,060 (six hundred sixty vigintillion, sixty septillion, sixty sextillion, sixty, which spelled backwards is ytxis noillitxes ytxis noillitpes ytxis noillitnigiv ytxis derdnuh xis).
62. 166
63. 242
64. (
, 
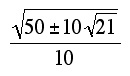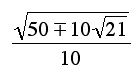) (i.e., there are two such points)
65. a) 111,111,111,113
b) 617,286
c) 54,869,686
d) 44,544,551
e) 11,111,111,111,111,111,111,111,111,122,222,222,222,222,222,222,222,233,333,333,348
f) 64
g) n = 5k2+2
h) 542,526
66. 8,281
67. a) 100
b) 0
68. a) 4,342,858,240
b) 6
69. 1107/2000, or .5535
70. (1, 25, 269, 2789, 27999, 289999, 2999999, 37999999, 379999999, 3899999999, 39999999999, 489999999999, 4899999999999, 49999999999999, 589999999999999, 5999999999999999, 69999999999999999, 699999999999999999, 7999999999999999999, 89999999999999999999, 999999999999999999999)
71. a) 18,888,888,888,888,888,888,888,888
b) 13 different values of n, the smallest of which is 37
72. a) 12 hr, 2 2/3 min (i.e., exactly 12:02:40) . . . 12 hr, 53 7/13 min (approximately 12:53:32) . . . 1 hr, 4 6/13 min (approximately 1:04:28)
b) 1 hr, 4 8/13 min (approximately 1:04:37) . . . 11 hr, 5 5/11 min (approximately 11:05:27) (Interestingly, for the latter question, the angle between the hands would be exactly 60 degrees.)
73. 9. They are:
{36}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 18}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 12}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 4, 9}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 6, 6}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 9}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 3, 6}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 4}
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 3, 3}
74. a) 1/5 b) 1/20 c) 1/20 d) 1/10 e) 1/10 f) 1/5 g) 1/20 h) 1/20 i) 1/10 j) 1/10
75. I counted 1,549.
76. a) the 134-digit number represented as a 2, followed by 100 5s, followed by 33 8s
b) the 105-digit number represented as a 6 followed by 104 9s
77. a) 51,515,158,585
b) 1,515,151,515,151,212,121,212,121
78. 698,989,898,989
79. 109
80. a) 20,200
b) 1,202,100
81. a) 25,569
b) 5899
82. 15,710,112
83. a) 10,761,679
b) 1
84. The 986,411-digit repunit; that is, the string 11,111, . . . , 111, with a total of 986,411 digits.
85. a) 100,000,000,011,111,112,222,222,333,333,444,445,555,666,778
b) the 100-digit number represented as five 9s, followed (in order) by six 8s, seven 7s, eight 6s, nine 5s, eleven [sic] 4s, twelve 3s, thirteen 2s, fourteen 1s, and fifteen 0s
86. d = 3,080,513,870,206,229,237; k = 468,015,010,283,520,000
87. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
88. 2.25 × 106
89. 801
90. a) 12
b) 10999,999,999
91. a) 6,198,089,008,491,993,412,800
b) 1,089,380,862,964,257,455,695,840,764,614,254,743,075
92. 2129
93. a) 368,748
b) 189
94. a) 2
b) 223
c) 988,861
95. a) 755,333,322,222,222. The product of its digits is 3,628,800, which is 10!.
b) 45,578,899, the product of whose digits is also 10!.
96. a) 91
b) 995,328
c) 9,696. The smallest is 26,666,688; the largest is 666,662,222,222.
97. a) 1.953%
b) 57.834%
c) 40.213%
98. a) 1,555,555,555,555,555,555,555,555,555,555,555
b)
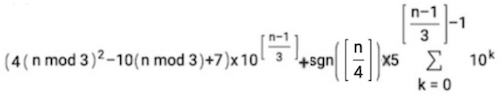
is a possibility, where square brackets [] represent the greatest integer function, and "sgn" is the sign (signum) function.
99. a) [log2(log2n)]+1 steps, where the square brackets [] represent the greatest integer function
b) 155 digits, the last of which is a 6
100. a) 33.995%
b) 37.538%
c) 28.467%
101. a) 93.9529%
b) 53.7399%
c) 6.0471%
102. 210
103. 32. They are 2, 3, 5, 7, 12, 21, 113, 115, 131, 151, 311, 511, 1112, 1121, 1211, 2111, 11113, 11117, 11131, 11171, 11311, 11711, 13111, 17111, 31111, 71111, 111112, 111121, 111211, 112111, 121111, and 211111.
104. 4
105. a) 244
b) 438,403
c) 22 46/61
d) 3 163/177
106. a) 6
b) 12
c) 57
d) 237
e) 349
f) 1396
107. a) 409 days, or about 13 1/2 months
b) 1317 days, or a little over 3 1/2 years
c) 2 minutes and 44 seconds
108. a) 2,499,999
b) 6,397,940
109. the 100-digit number represented as 73 9s, followed (in order) by five 8s, four 7s, two 6s, four 5s, two 4s, four 3s, four 2s, one 1, and one 0
110. 19/2 n – 1/2 n2, for 1 < n < 10 ;
no solution, for n > 10
111. the number with 113,717,421 digits, all of which are 9s; that is, 10113,717,421–1
112. the 113,717,426-digit number whose digits, left to right, are 102345678, followed by 113,717,417 9s
113. a) (68,34)
b) (147,49)
c) (99,11)
d) Two solutions: (98,49) and (147,49)
114. 945n/10
115. a) 1 in 14,028
b) 1 in 4
c) 1 in 351
d) 1 in 4
e) 1 in 305
f) 1 in 85
g) 1 in 334
h) 1 in 4
i) 1 in 369
j) 1 in 4
116. 17
117. As far as I have been able to determine, n = 1125. For all L>3, S1125,L = 8L–24.
118. a) 2/85 (two eighty-fifths)
b) 85/86 (eighty-five eighty-sixths)
119. 120
120. 20
121. 38
122. 30,000
123. 109
124. a) 131
b) 8. They are 68, 86, 246, 264, 426, 462, 624, and 642.
c) 2. They are 888 and 222,222,222.
125. 108
126. a) 9
b) 539,280. The smallest is 156,789; the largest is 876,543,210.
127. a) 11/11/2111
b) 11/15/2111
c) 12/27/2112
d) 12/29/2127
e) 12/29/2289
f) 12/29/4999
128. a) 05/26/1934
b) 2997 out of 36,525, or 999/12175, which is approximately 8.205%
c) 1 out of 36,525. There is only one such date: 11/11/1911.
d) 109 out of 36,525 (all such dates are in the year 2000)
129. 01/01/2000; 10/10/1600
130. 06/25/1987; 06/17/2345
131. a) 142
b) 1565
132. a) The 99-digit number represented as 78 9s, followed by 3 3s, followed by 18 1s. The sum of the digits is 729, which is 36; the product of the digits is 3159.
b) The 73-digit number represented as four 3s followed by 69 1s. The sum and product of the digits are both 81, which is 34.
133. 224,606
134. 2,142,584,059,011,987,034,055,949,456,454,883,470,029,603,991,710,390,447,068,500