Phi — The Ubiquitous Golden Ratio
Phi, a number of which almost no one has heard, is, to me, the most ubiquitous and interesting number in existence. As my description of it as being "ubiquitous" implies, it seems to turn up almost everywhere, especially when it's least expected.
At this point, the obvious question would seem to be: "What is phi?"
Phi is an irrational number (a number that cannot be expressed in decimal form) whose value is 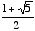 . Its approximate decimal value is 1.61803398. Some mathematicians call it "tau." However, for the sake of consistency, I shall hereafter always refer to it as phi.
. Its approximate decimal value is 1.61803398. Some mathematicians call it "tau." However, for the sake of consistency, I shall hereafter always refer to it as phi.
Phi was named after the Greek sculptor Phidias by American mathematician Mark Barr. The Greek cursive symbol for phi is " ," which I will use frequently throughout this paper. The ratio between
," which I will use frequently throughout this paper. The ratio between 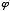 and 1 is often called "the golden ratio." The line segment shown below is divided so that the ratio of its total length to the length of segment "A" is the golden ratio, as is the ratio between the lengths of segments "A" and "B:"
and 1 is often called "the golden ratio." The line segment shown below is divided so that the ratio of its total length to the length of segment "A" is the golden ratio, as is the ratio between the lengths of segments "A" and "B:"

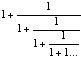
As can most irrational numbers, phi can be expressed as the sum of an infinite series — in fact each of several infinite series can express phi. Here are two of them — notice their simplicity:
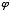 =
= 
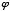 =
= 
Another interesting and important characteristic of phi is that its reciprocal is one less than phi itself. This can easily be shown on a slide rule, and each of the following equations proves it algebraically:
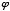 =
= 
Multiply by 2 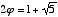
Subtract 1 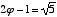
Square 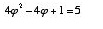
Subtract 1 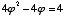
Divide by 4 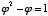
Divide by 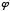

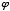 =
= 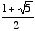
Subtract 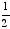
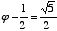
Square 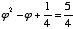
Subtract 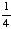
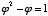
Divide by 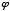
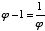
However, if one does not know the value of phi as being 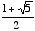 , but is looking for the value of x where
, but is looking for the value of x where 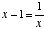 , he may reverse either of the two equations shown above,* or use the easier method of solving it by quadratic, in this manner:
, he may reverse either of the two equations shown above,* or use the easier method of solving it by quadratic, in this manner:
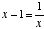
Multiply by x 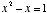
Subtract 1 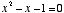
* this, of course, is virtually impracticable, due to the fact that he would, most likely, be required to know the value, to be able to proceed in the proper order
This equation obviously cannot be factored, so it must be solved by using the quadratic formula:
If 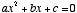 ,
,
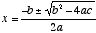 .
.
In the equation (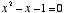 ), a would be 1, b would be –1, and c would be –1. Substituting these values for a, b, and c in the quadratic equation, we have
), a would be 1, b would be –1, and c would be –1. Substituting these values for a, b, and c in the quadratic equation, we have 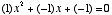 , so that:
, so that:
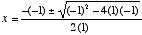
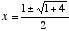
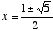 ,
,
whose positive value would be phi, and whose negative value would be  , which, like phi, is one greater than its reciprocal,
, which, like phi, is one greater than its reciprocal,  .
.
Another important use of phi is in geometry. It is interesting to note that the ratio of the length of the radius of a circle to that of a side of an inscribed regular decagon (a regular decagon [10-sided polygon] placed inside the circle with its corners touching the circumference of the circle) is the golden ratio. Why is this true? The formula for finding ratios between lengths of radii of circles and those of inscribed regular polygons explains this. It is:
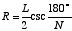 ,
,
where R is the radius of the circle, L is the length of a side of the inscribed polygon, and N is the number of sides in the polygon. "csc," by the way, is the abbreviation used in trigonometry for "cosecant." The cosecant of an angle is the ratio between the length of the hypotenuse (longest side) to the side opposite the hypotenuse in a right triangle, when the given angle is the one between the hypotenuse and the side adjacent to the hypotenuse; that ratio is determined by the size of that angle.
Substituting 10 for N, the equation can be worked in this manner:
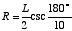
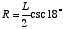

Divide by L 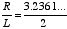
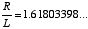
The value 3.2361... for the cosecant of an 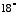 angle can be found by using a slide rule or by referring to a table of cosecants. 1.61803398... is, of course, phi.
angle can be found by using a slide rule or by referring to a table of cosecants. 1.61803398... is, of course, phi.
But that is not phi's only use in geometry. Geometric figures based on the golden ratio can be constructed. A golden rectangle, for instance, is a rectangle in which the ratio of the length to the width is the golden ratio. If three such rectangles are placed in intersection, each rectangle perpendicular to the other two, the corners of the resulting figure coincide with the corners of a regular icosahedron (20-sided polyhedron) or the centers of the faces of a dodecahedron (12-sided polyhedron). Another very interesting characteristic of a golden rectangle is that if a perfect square is "chopped off" of one end, a golden rectangle still remains. A golden rectangle is the only rectangle that could possess this characteristic. This can be proven by solving for x in the equation:
 ,
,
where 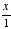 is the ratio of the length of the original rectangle to its width,
is the ratio of the length of the original rectangle to its width,  is the length-to-width ratio of the square, and
is the length-to-width ratio of the square, and 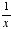 is this ratio in the resulting figure. A little figuring shows this to yield the quadratic (
is this ratio in the resulting figure. A little figuring shows this to yield the quadratic (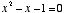 ), which was solved earlier as
), which was solved earlier as 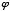 and
and 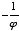 . However, the root
. However, the root  must be rejected in this case, since rectangles cannot have negative dimensions.
must be rejected in this case, since rectangles cannot have negative dimensions.
Another use of phi in geometry is the golden triangle. This is an isosceles triangle in which the ratio of the length of a side to that of the base is the golden ratio. Curiously enough, in a golden triangle, the base angles would be 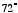 , and the top angle,
, and the top angle, 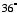 . This is the only triangle in which the base angles are twice the top angle. Curious to find the measures of the angles in a triangle in which the base angles would be at golden ratio to the top angle, I set up this equation:
. This is the only triangle in which the base angles are twice the top angle. Curious to find the measures of the angles in a triangle in which the base angles would be at golden ratio to the top angle, I set up this equation:
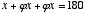
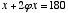
—> 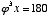
Divide by 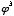
 = top angle
= top angle
 = base angle
= base angle
If the arrowed step in which I added 1 and 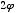 (the respective coefficients of x) to receive
(the respective coefficients of x) to receive 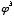 seems questionable, I will attempt to clear that up in discussing phi's relation to additive series. . . .
seems questionable, I will attempt to clear that up in discussing phi's relation to additive series. . . .
An additive series is a series of numbers in which the value of each is the sum of an established number of preceding numbers, and in the most frequently used additive series, the sum of the two preceding numbers (e.g., 3, 8, 11, 19, 30, 49, 79, 128, 207, 335, etc.). But an interesting phenomenon occurs. No matter what the starting numbers, any additive series in which each term is the sum of the two preceding it strives to obtain the golden ratio between each term and the one preceding it. As the series progresses, this ratio gets closer and closer to phi, alternately higher and lower, but, alas, the "try" is in vain for all additive series, except one. It starts with 1, and then phi. Their sum is 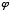 +1. This would continue as follows:
+1. This would continue as follows:
(1,  ,
, 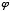 +1, 2
+1, 2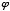 +1, 3
+1, 3 +2, 5
+2, 5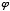 +3, 8
+3, 8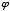 +5, 13
+5, 13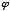 +8, etc.).
+8, etc.).
But those numbers can be expressed differently. Any number raised to the zero power, of course, is 1. So we may substitute  for 1. Also, any number to the first is itself, so we can say
for 1. Also, any number to the first is itself, so we can say 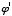 instead of
instead of 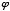 . So now we have, instead of (1,
. So now we have, instead of (1,  ), (
), (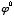 ,
, 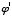 ). The exponents are increasing by one. Now, is
). The exponents are increasing by one. Now, is  ? Yes, it is — I discovered this proof:
? Yes, it is — I discovered this proof:
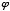 =
= 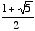
Multiply by 2 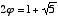
Subtract 1 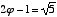
Square 
Subtract 1 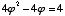
Divide by 4 
Add 
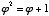
Or, should we look for a number "x" so that 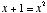 , we would again end up with the quadratic (
, we would again end up with the quadratic (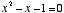 ), whose positive solution has been fairly well established as being phi.
), whose positive solution has been fairly well established as being phi.
Some figuring will show that this trend of exponents to increase by 1 will continue, so that (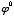 ,
, 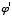 ,
, 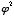 ,
, 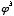 ,
, 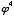 ,
, 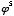 ,
,  ,
, 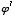 ,
, 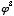 ,
, 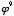 ,
, 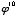 , etc.) is, indeed, an additive series, and identical to the one given above. Each term is the sum of the two preceding it. As a general rule, one could state:
, etc.) is, indeed, an additive series, and identical to the one given above. Each term is the sum of the two preceding it. As a general rule, one could state:
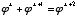 .
.
Therefore  ,
, 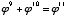 , and
, and  . But probably the most important characteristic is the fact that the ratio between any number in this series and the one before it is constant. That ratio is, of course, phi. Not only is this additive series (in which each term is the sum of the two preceding it) the only one in which the ratio between adjacent terms is constant, but phi is the only ratio at which a "2-term" additive series could be constant. However, an additive series in which each term is the sum of the preceding three (e.g., 1, 4, 5, 10, 19, 34, etc.) tends to approach a different ratio, approximately 1.8395, and a "4-term" additive series approaches about 1.9275. But these numbers are not as ubiquitous as phi.
. But probably the most important characteristic is the fact that the ratio between any number in this series and the one before it is constant. That ratio is, of course, phi. Not only is this additive series (in which each term is the sum of the two preceding it) the only one in which the ratio between adjacent terms is constant, but phi is the only ratio at which a "2-term" additive series could be constant. However, an additive series in which each term is the sum of the preceding three (e.g., 1, 4, 5, 10, 19, 34, etc.) tends to approach a different ratio, approximately 1.8395, and a "4-term" additive series approaches about 1.9275. But these numbers are not as ubiquitous as phi.
It has been discovered that many Renaissance artists quite deliberately used the golden ratio in their paintings. One mathematician claims that 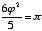 (pi). This value, instead of the well known 3.141592653589793128426..., is approximately 3.14164078644620550. And one imaginative mathematician claims that the ratio of the height of the average woman to the height above the floor of her navel is the golden ratio.
(pi). This value, instead of the well known 3.141592653589793128426..., is approximately 3.14164078644620550. And one imaginative mathematician claims that the ratio of the height of the average woman to the height above the floor of her navel is the golden ratio.
Phi is truly ubiquitous!
Bibliography
Gardner, Martin, The 2nd "Scientific American" Book of Mathematical Puzzles & Diversions, Simon and Schuster, 1961
Handbook of Chemistry and Physics, Chemical Rubber, 1942
Also, many thanks to James King and Samuel Rhodes for their help in supplying me with information.
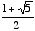 . Its approximate decimal value is 1.61803398. Some mathematicians call it "tau." However, for the sake of consistency, I shall hereafter always refer to it as phi.
. Its approximate decimal value is 1.61803398. Some mathematicians call it "tau." However, for the sake of consistency, I shall hereafter always refer to it as phi. ," which I will use frequently throughout this paper. The ratio between
," which I will use frequently throughout this paper. The ratio between 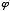 and 1 is often called "the golden ratio." The line segment shown below is divided so that the ratio of its total length to the length of segment "A" is the golden ratio, as is the ratio between the lengths of segments "A" and "B:"
and 1 is often called "the golden ratio." The line segment shown below is divided so that the ratio of its total length to the length of segment "A" is the golden ratio, as is the ratio between the lengths of segments "A" and "B:"
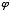 =
= 
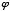 =
= 
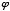 =
= 
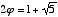
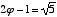
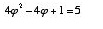
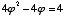
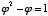
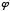

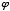 =
= 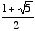
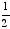
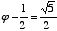
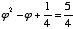
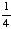
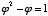
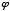
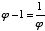
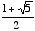 , but is looking for the value of x where
, but is looking for the value of x where 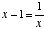 , he may reverse either of the two equations shown above,* or use the easier method of solving it by quadratic, in this manner:
, he may reverse either of the two equations shown above,* or use the easier method of solving it by quadratic, in this manner: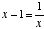
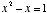
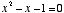
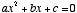 ,
,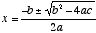 .
.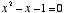 ), a would be 1, b would be –1, and c would be –1. Substituting these values for a, b, and c in the quadratic equation, we have
), a would be 1, b would be –1, and c would be –1. Substituting these values for a, b, and c in the quadratic equation, we have 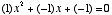 , so that:
, so that: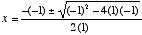
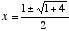
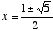 ,
, , which, like phi, is one greater than its reciprocal,
, which, like phi, is one greater than its reciprocal,  .
.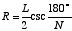 ,
,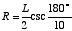
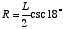

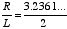
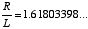
 angle can be found by using a slide rule or by referring to a table of cosecants. 1.61803398... is, of course, phi.
angle can be found by using a slide rule or by referring to a table of cosecants. 1.61803398... is, of course, phi. ,
,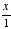 is the ratio of the length of the original rectangle to its width,
is the ratio of the length of the original rectangle to its width,  is the length-to-width ratio of the square, and
is the length-to-width ratio of the square, and 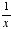 is this ratio in the resulting figure. A little figuring shows this to yield the quadratic (
is this ratio in the resulting figure. A little figuring shows this to yield the quadratic (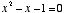 ), which was solved earlier as
), which was solved earlier as 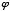 and
and 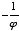 . However, the root
. However, the root  must be rejected in this case, since rectangles cannot have negative dimensions.
must be rejected in this case, since rectangles cannot have negative dimensions.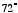 , and the top angle,
, and the top angle, 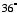 . This is the only triangle in which the base angles are twice the top angle. Curious to find the measures of the angles in a triangle in which the base angles would be at golden ratio to the top angle, I set up this equation:
. This is the only triangle in which the base angles are twice the top angle. Curious to find the measures of the angles in a triangle in which the base angles would be at golden ratio to the top angle, I set up this equation: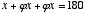
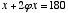
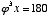
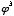
 = top angle
= top angle = base angle
= base angle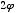 (the respective coefficients of x) to receive
(the respective coefficients of x) to receive 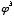 seems questionable, I will attempt to clear that up in discussing phi's relation to additive series. . . .
seems questionable, I will attempt to clear that up in discussing phi's relation to additive series. . . .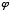 +1. This would continue as follows:
+1. This would continue as follows: ,
, 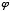 +1, 2
+1, 2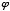 +1, 3
+1, 3 +2, 5
+2, 5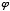 +3, 8
+3, 8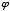 +5, 13
+5, 13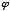 +8, etc.).
+8, etc.). for 1. Also, any number to the first is itself, so we can say
for 1. Also, any number to the first is itself, so we can say 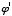 instead of
instead of 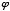 . So now we have, instead of (1,
. So now we have, instead of (1,  ), (
), (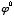 ,
, 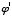 ). The exponents are increasing by one. Now, is
). The exponents are increasing by one. Now, is  ? Yes, it is — I discovered this proof:
? Yes, it is — I discovered this proof: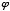 =
= 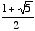
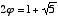
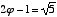

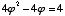


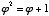
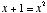 , we would again end up with the quadratic (
, we would again end up with the quadratic (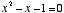 ), whose positive solution has been fairly well established as being phi.
), whose positive solution has been fairly well established as being phi.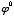 ,
, 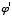 ,
, 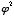 ,
, 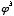 ,
, 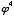 ,
, 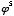 ,
,  ,
, 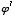 ,
, 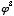 ,
, 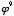 ,
, 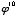 , etc.) is, indeed, an additive series, and identical to the one given above. Each term is the sum of the two preceding it. As a general rule, one could state:
, etc.) is, indeed, an additive series, and identical to the one given above. Each term is the sum of the two preceding it. As a general rule, one could state: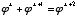 .
. ,
, 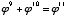 , and
, and  . But probably the most important characteristic is the fact that the ratio between any number in this series and the one before it is constant. That ratio is, of course, phi. Not only is this additive series (in which each term is the sum of the two preceding it) the only one in which the ratio between adjacent terms is constant, but phi is the only ratio at which a "2-term" additive series could be constant. However, an additive series in which each term is the sum of the preceding three (e.g., 1, 4, 5, 10, 19, 34, etc.) tends to approach a different ratio, approximately 1.8395, and a "4-term" additive series approaches about 1.9275. But these numbers are not as ubiquitous as phi.
. But probably the most important characteristic is the fact that the ratio between any number in this series and the one before it is constant. That ratio is, of course, phi. Not only is this additive series (in which each term is the sum of the two preceding it) the only one in which the ratio between adjacent terms is constant, but phi is the only ratio at which a "2-term" additive series could be constant. However, an additive series in which each term is the sum of the preceding three (e.g., 1, 4, 5, 10, 19, 34, etc.) tends to approach a different ratio, approximately 1.8395, and a "4-term" additive series approaches about 1.9275. But these numbers are not as ubiquitous as phi.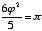 (pi). This value, instead of the well known 3.141592653589793128426..., is approximately 3.14164078644620550. And one imaginative mathematician claims that the ratio of the height of the average woman to the height above the floor of her navel is the golden ratio.
(pi). This value, instead of the well known 3.141592653589793128426..., is approximately 3.14164078644620550. And one imaginative mathematician claims that the ratio of the height of the average woman to the height above the floor of her navel is the golden ratio.